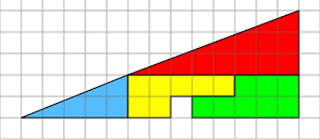
Mettiamo di avere un triangolo rettangolo avente due cateti di 13 e 5 cm, diviso in quattro parti colorate. Per praticità facciamo come ai tempi delle elementari e lo disegniamo su un foglio a quadretti magari preso in prestito dal compagno di banco.
Ecco otteniamo un triangolo simile a questo.
Adesso spostiamo le parti colorate e andiamo a costruire un altro triangolo rettangolo avente sempre due cateti di 13 e 5 cm ma qualcosa non torna manca un quadrato.
Dove è sparita la parte mancante?
La soluzione

l'è un mistero!
RispondiEliminaconta qualcosa il fatto che i due triangoli in realtà abbiamo inclinazioni diverse? 2x5 il primo, 3x8 il secondo... che dovrebbe essere 3x7.5 per avere la stessa inclinazione. è solo un'illusione?
RispondiEliminagrande intuizione, però manca qualcosina ancora...
RispondiEliminaPerchè a differenza di quanto hai premesso, non hai disegnato un triangolo rettangolo rettangolo con i cateti di 13 e 5 cm, ma semplicemente due triangoli (non simili fra loro) e altri due poligoni aventi dei lati adiacenti che posso "illudere" l'osservatore facendo pensare che la figura complessiva sia un triangolo rettangolo. Di fatto considerando i quadratini come unità di misura (di aree) non è sparito nulla: le superfici delle due figure sono uguali. Non è un triangolo la figura complessiva precedente e non è un triangolo la figura successiva... sono ambedue dei poligoni... nulla di strano. L.
RispondiEliminaCiao L.
RispondiEliminaesattemente, sono poligoni come spiegato nella soluzione :)
Anche con la soluzione rimango perplessa...
RispondiEliminaIl triangolo rosso è più lungo e più
RispondiEliminaalto, Spostando i triangoli avviene
l'ammanco.rimettendoli a posto, tutto torna regolare.